Most basic violin plot in d3.js




A violin plot is an alternative to the more usual boxplot, especially interesting with large dataset where boxplot could hide a part of the information. Here is a simple implementation in d3.js using the d3.histogram() function, keeping only the core code to understand the fundamental concept.


Violin plot section

Steps:

  • It is important to understand that this violin plot is made using the d3.histogram() function, not using a kernel density estimate.

  • It takes the values of a group and split it in several bins. The number of value observed in each bin is represented, and a curve is used for smoothing.

  • The size of each bin is controlled by the thresholds argument of the d3.histogram() function. It is advised to try different bin size.

  • Here, the highest number of item per bin is computed. This value will as wide as 100% of the bandwidth. So you just have to play with the padding argument of the x axis to control space between violin.

  • Note: With this method, a group with less values than another will have a smaller width.
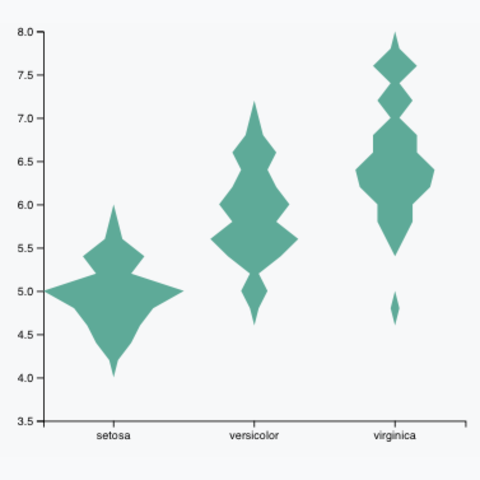
<!DOCTYPE html>
<meta charset="utf-8">

<!-- Load d3.js -->
<script src="https://d3js.org/d3.v4.js"></script>

<!-- Create a div where the graph will take place -->
<div id="my_dataviz"></div>


<script>

// set the dimensions and margins of the graph
var margin = {top: 10, right: 30, bottom: 30, left: 40},
    width = 460 - margin.left - margin.right,
    height = 400 - margin.top - margin.bottom;

// append the svg object to the body of the page
var svg = d3.select("#my_dataviz")
  .append("svg")
    .attr("width", width + margin.left + margin.right)
    .attr("height", height + margin.top + margin.bottom)
  .append("g")
    .attr("transform",
          "translate(" + margin.left + "," + margin.top + ")");

// Read the data and compute summary statistics for each specie
d3.csv("https://raw.githubusercontent.com/holtzy/D3-graph-gallery/master/DATA/iris.csv", function(data) {

  // Build and Show the Y scale
  var y = d3.scaleLinear()
    .domain([ 3.5,8 ])          // Note that here the Y scale is set manually
    .range([height, 0])
  svg.append("g").call( d3.axisLeft(y) )

  // Build and Show the X scale. It is a band scale like for a boxplot: each group has an dedicated RANGE on the axis. This range has a length of x.bandwidth
  var x = d3.scaleBand()
    .range([ 0, width ])
    .domain(["setosa", "versicolor", "virginica"])
    .padding(0.05)     // This is important: it is the space between 2 groups. 0 means no padding. 1 is the maximum.
  svg.append("g")
    .attr("transform", "translate(0," + height + ")")
    .call(d3.axisBottom(x))

  // Features of the histogram
  var histogram = d3.histogram()
        .domain(y.domain())
        .thresholds(y.ticks(20))    // Important: how many bins approx are going to be made? It is the 'resolution' of the violin plot
        .value(d => d)

  // Compute the binning for each group of the dataset
  var sumstat = d3.nest()  // nest function allows to group the calculation per level of a factor
    .key(function(d) { return d.Species;})
    .rollup(function(d) {   // For each key..
      input = d.map(function(g) { return g.Sepal_Length;})    // Keep the variable called Sepal_Length
      bins = histogram(input)   // And compute the binning on it.
      return(bins)
    })
    .entries(data)

  // What is the biggest number of value in a bin? We need it cause this value will have a width of 100% of the bandwidth.
  var maxNum = 0
  for ( i in sumstat ){
    allBins = sumstat[i].value
    lengths = allBins.map(function(a){return a.length;})
    longuest = d3.max(lengths)
    if (longuest > maxNum) { maxNum = longuest }
  }

  // The maximum width of a violin must be x.bandwidth = the width dedicated to a group
  var xNum = d3.scaleLinear()
    .range([0, x.bandwidth()])
    .domain([-maxNum,maxNum])

  // Add the shape to this svg!
  svg
    .selectAll("myViolin")
    .data(sumstat)
    .enter()        // So now we are working group per group
    .append("g")
      .attr("transform", function(d){ return("translate(" + x(d.key) +" ,0)") } ) // Translation on the right to be at the group position
    .append("path")
        .datum(function(d){ return(d.value)})     // So now we are working bin per bin
        .style("stroke", "none")
        .style("fill","#69b3a2")
        .attr("d", d3.area()
            .x0(function(d){ return(xNum(-d.length)) } )
            .x1(function(d){ return(xNum(d.length)) } )
            .y(function(d){ return(y(d.x0)) } )
            .curve(d3.curveCatmullRom)    // This makes the line smoother to give the violin appearance. Try d3.curveStep to see the difference
        )
})

</script>

Variation

It is important to understand that in the violin chart above the smoothing effect is due to a curve interpolation between bins. Here is the result without any interpolation (left) and using a curveStep interpolation (right). Just change the .curve() call in the code above to get these results.

Related blocks →